2000年11月15日 – 東京 – 日経金融新聞 金融フロンティア
手術室をのぞいてみよう
十年前は珍しかった金融シミュレーションも、今ではありふれてプライシングやリスク計測に使われている。しかし、計算過程の理解は大変だ。このため、モデルの信頼性保証は、勢いシステム会社や設計者の手にゆだねられ、患者と医者に似た関係が生まれてしまう。だからと言って、手術内容に患者が無関心でいてよいはずはない。
そこで本稿では、医療事故になりかねない金融数学の事例を集めてみた。
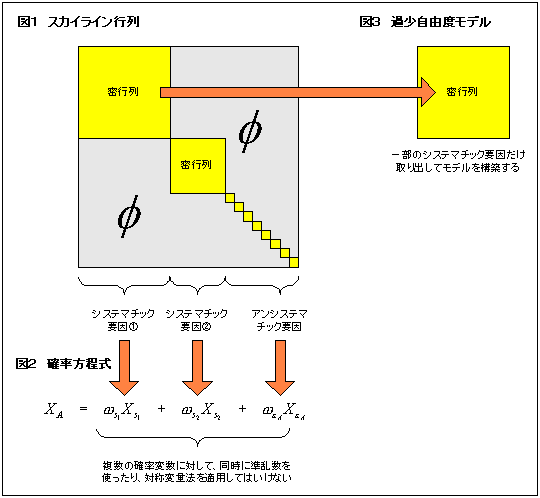
1. 過少自由度の設計
複数の確率変動要因間の関係は、線型代数学の助けを借りて実対称行列で表現できる（図1）。図の斜線部は密行列（非零の領域）であり、金融ではシステマチックリスクと呼ぶことがある。密行列を複数内包する行列形式がスカイライン行列で、確率変動モデルの典型的形状だ。実対称行列の一辺の長さ（行列の次元数）が自由度で、内包する密行列および対角成分に応じた確率変数を右辺に置いて、確率方程式を組み立てる（図2）。これは金融に限らず構造解析をはじめとする他のシミュレーション分野でも同じである。話について来ていない方も「そんなものだ」と思ってほしい。
さて問題はここからだ。大きな自由度を扱うには、それなりに面倒なテクニック（数値計算法と言う）が必要だ。このため、意図的に自由度を少なくして計算をサボるケースをよく見かける。一時期流行したリスクメトリックスもそのひとつ（図3）。ひどい例では三千銘柄超の個別株を一確率変数で表現し、大きな誤差を伴うモデルさえ存在する。
国際ルール化している当局規制も、確信犯的に過少自由度を認めている。規制の裏をかくのはとても簡単、自由度不足の場所にスプレッドポジションでも作ればよい。「国際決済銀行（BIS）基準対応のVaR（バリュー・アット・リスク）を使えばリスク管理は万全」的発想は危ないのである。
2. 不安定な三角分解操作
実利主義・結果至上の金融屋の数学は、数学者からよく揶揄（やゆ）される物理学者の数学以上に杜撰（ずさん）だと思う。私自身も銀行員時代を含めて反省する点が多々ある。
シミュレーションの過程では先の密行列に対し、単変量で言う平方根操作、L・Lt形式への変換、つまり三角分解が必要だ。ところが、ここに入門書でよく紹介されるコレスキー分解法を使う場合、個々の数字が同じ方向に動きがちな金融系列（例・短期金利）を多数扱ったりすると、計算中にエラーが起こることがある。そんなモデルは、時々「妙に数字が狂う」。専門用語で言えばロバスト（強固）でない。この問題を抱えたシステムは計算を繰り返すほど間違いが多く生じる。だから相関係数を毎日見直すような使い方を禁止していたりする。
詳細は解説が長くなるので省くけれども、入門書から一歩進んで勉強すれば、まずL・D・Lt形式に変換してからL・Lt形式に向かう行列操作が適切とわかるだろう。
3. 収束性改善策の乱用
収束性改善策は見かけ上の誤差を減少させる。しかし、その副作用、系列間相関（マルチコ）や準乱数周期の弊害も大きい（図2）。「だれがこんな人にPh.D.を与えたのか」と笑い話ができるほど、この種の統計学上の誤り（Type I Error、通称「慌てもののエラー」）にははまりやすい。たとえば、とある著名なリスク管理システム会社の方からさえ、「準乱数（乱数に似た数列）により、数万件のポートフォリオを相手に、五千回以下の試行回数で市場・信用イベント同時存在下のリスク量を計算可能」と主張されて、閉口したことさえある。
数値シミュレーションの性格上、実用精度に到達するのは、単体イベントの計測でも一万回級、同時イベントならば、さらに多くの計算試行の末である。合併銀行の巨大資産さえ、十万回の計算をPCサーバーが十七時間（四CPUのLinuxサーバーで測定、信用VaR、CVaR、リスクコントリビューション、OLAP、DM／MTMを同時計算）で完了する今日でも、相応の準備が必要だ。
100,000回シミュレーション+収束性改善策による滑らかなPDF（確率密度分布図）
同、与信分散効果のXYプロット図
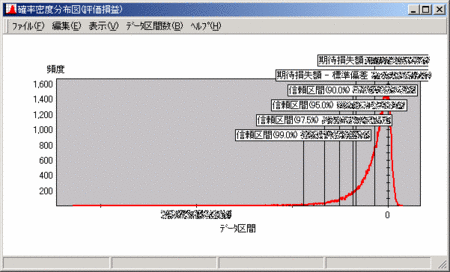
事後点検の勧め
今や成功率90%以上、手術台で患者が亡くなれば心臓外科医の腕がまず疑われる冠動脈バイパス手術も、昔ははるかに危険な施術であった。数年前、「専門家」に依頼した高額なモデル監査も結構怪しい。中古建築と同じく、モデルやシステムの品質は利用者自身が見極める他に方法はない。
